Sorting
Pieces of this lab were adapted from a prior sorting lab by R. Jordan Crouser. This lab was updated by Alicia M. Grubb in Spring 2019/2020.
Repeat Warning
In order to be sucessful in computer science, an important skill that you must develop is understanding how to implement and develop a specification, and knowing when you can take liberty with the specification. You also need to distingush between implementing and developing a specification. In the course work for CSC111, we ask for some things very precisely. It is important that you read every word of lab and assignment descriptions. Misreading or ignoring directions will result in incorrect software/code.
In this lab, we’ll continue learning about sorting.
Step 0: Refresher
Create a new file/document in Thonny and save it locally with the file name lab9.py. Add the course header with the relavent information.
In class we looked at three different sorting algorithms (selection and bubble sort). In this lab we are going to review these algorithms and focus on how they are built. These algorithms allow you to manipulate python lists and other iterables (i.e. things that you can iterate over). For today, we’ll just focus on sorting ints, but you can sort any data type that can be compared with a “>”-like operation.
Although python has built-in sorting methods which we’ll see a little later, we’ll start by implementing a few of our own from scratch.
Step 1: Selection Sort
Let’s consider one approach to sorting: SelectionSort. This algorithm works by finding the smallest not-yet-sorted element, and then we swap it with whatever element is in its “spot”:
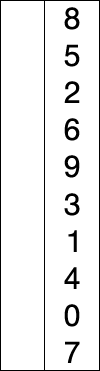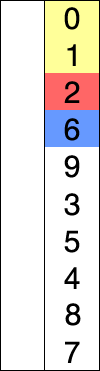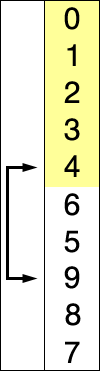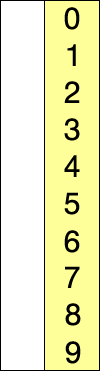
This process consists of finding the smallest elements and swapping the element.
Step 1A: Swapping Elements
Begin by writing a function to swap two elements in a list, given the following function definition:
def swap(iList, i1, i2):where i1 and i2 are the indexes of the elements to swap, and iList is the list.
For example,
>>> myList = [8,3,6,2,9,1]
>>> swap(myList, 1, 2)
>>> print(myList)
[8, 6, 3, 2, 9, 1]Note: If you are having trouble with this function, practice by first writing the code to swap the values held in two variables. For example:
x = 6
y = 9
## TODO write code that will move the value from x into y and the value from y into x.
## Hint: Introduce a third, temporary, variable.Write five interesting test cases for swap with assertions (assert) to your main. For example,
def main():
testList = [8,3,6,2,9,1]
swap(testList, 1, 2)
assert testList == [8, 6, 3, 2, 9, 1]
## TODO write additional test cases here...Step 1B: Find Smallest Element In A SubList
Next define a function that finds the index of the smallest element in a sublist, given by the following function definition:
def findIndexOfSmallest(iList, start, stop):where you find the smallest element in iList between start up to, but not including stop.
For example,
>>> myList = [28,26,23,22,29,21]
>>> print(findIndexOfSmallest(myList,2,4))
3
>>> print(findIndexOfSmallest(myList,2,6))
5Try to complete this without copying/pasting code from your notes. Think of a method that is closer to how a human would scan a list left to right keeping track of the minimum they’ve seen so far and changing it each time they see a smaller number.
Write five interesting test cases for findIndexOfSmallest with assertions (assert) to your main.
Step 1C: Selection Sort Function
Next add the following function below the two you defined above.
def selectionSort(iList):
for i in range(len(iList)):
iSmall = findIndexOfSmallest(iList, i, len(iList))
swap(iList, i, iSmall)Test your selection sort with a few examples, such as
[8,6,3,2,9,1]
[12,11,10,9,8,7,6,5,4,3,2,1]
[1,2,4,5,6,7,0]Write five interesting test cases for selectionSort with assertions (assert) to your main.
Step 1D: Discussion
Begin by downloading the short answer starter file (click this link), and save it locally. Open the file with either Thonny or a text editor. Answer the following short answer question (1-2 English sentences.):
- SA Question #1: What happens if you change the line:
swap(iList, i, iSmall)to beswap(iList, iSmall, i)? - SA Question #2: Why do we need to add the for loop over the range of the length of the list?
- SA Question #3: What would you have to change to sort the list from largest item to smallest item?
- SA Question #4: Why is the input to
findIndexOfSmallestinclude bothiandlen(iList)? Why is this range necessary?
Step 2: Bubble Sort
The next sorting algorithm we’ll consider today is called bubbleSort, so named because of how smaller elements “bubble” to the top of the list (while larger elements “sink” to the bottom). In bubbleSort, adjacent elements are compared and (if found to be out of order), swapped. This process is repeated until the list is sorted, resulting in something like this:
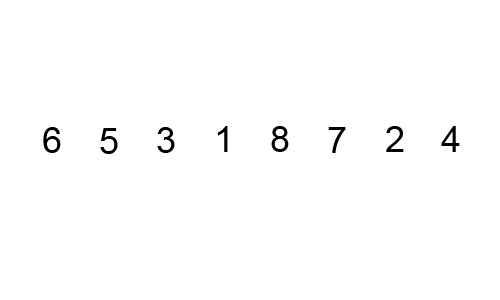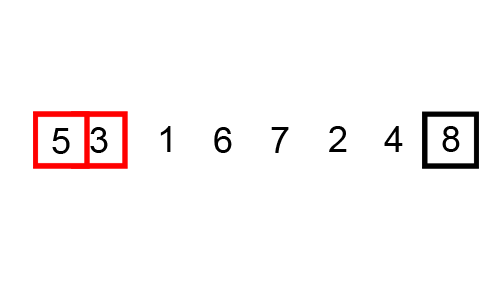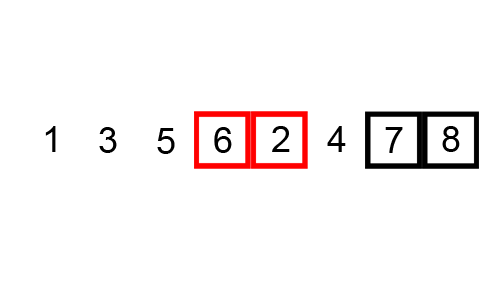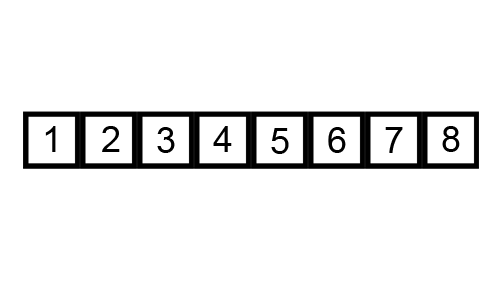
Step 2A: Bubble Function
Next we will write a function to bubble.
For each index p in the range [0, ..., n-2] of the list:
If item in position p is greater than item in position p+1:
Swap them with our swap function above.Your function should have the following definition:
def bubble(iList, iLen):Where iList is the list you are going to bubble over and iLen is the length of the list.
Notice that the largest element moved to the end of the list.
>>> myList = [10,8,6,3,2,9,1]
>>> bubble(myList, len(myList))
>>> print(myList)
[8, 6, 3, 2, 9, 1, 10]Using the bubble function one element is sorted.
Write five interesting test cases for bubble with assertions (assert) to your main.
Step 2B: Bubble Sort Function:
To write the Bubble Sort function, all we need to do is call bubble repeatedly (once for each element in the list):
def bubbleSort(iList):
for i in range(len(iList) - 1):
bubble(iList, len(iList))Test your bubble sort with a few examples, such as
[8,6,3,2,9,1]
[12,11,10,9,8,7,6,5,4,3,2,1]
[1,2,4,5,6,7,0]Write five interesting test cases for bubbleSort with assertions (assert) to your main.
Step 2C: Optimize Bubble Sort
Next we look at where in the algorithm the work is completed.
Answer the following questions in your lab9SA.txt file. Note: There are no questions numbered 5 through 10.
- SA Question #11: Why is it that we use
len(iList) - 1in the range function? What happens if we made itlen(iList)? - SA Question #12: For each of the following lists, calculate how many times we call the Bubble function?
A. [8,6,3,2,9,1] B. [12,11,10,9,8,7,6,5,4,3,2,1] C. [1,2,4,5,6,7,10] D. [10,1,2,4,5,6,7]
- SA Question #13: What general expression describes how many times we call the Bubble function (given the number of elements in the list).
We can reduce some of the work that python is doing in the Bubble Sort algorithm. For each additional iteration, reduce the size of the list that we call Bubble on. The optumBubbleSort function calls the Bubble function a minimum number of times, but achieves the same functionality as the Bubble sort function:
def optumBubbleSort(iList):
end = len(iList) - 1
while end != 0:
bubble(iList, end+1)
end = end - 1SA Question #14: What is the purpose of the second parameter in the Bubble function?
SA Question #15: How does the size of the list vary with each iteration of the loop.
SA Question #16: Describe what happens if the algorithm is given an already-sorted list (case C), or a partially sorted list where just the maximum value is not in the highest position (case D).
Lab Submission
- For this lab you need to submit your programs via Moodle. Go to our Moodle Page and submit your
lab9SA.txt, andlab9.pyfiles.