The original version was written by R. Jordan Crouser at Smith College, and it has been updated in January 2019/2020 by Alicia M. Grubb.

If you have not already done so, pick up your name card and find a new partner.

Breaking the Ice

Before begining the lab, take 2-3 minutes and get to know your lab partner. Do you like pets (cat/dogs/others)? What was the most recent movie you saw in theatres?

Warm Up: Understanding how Floats take over.

In this opening section, we’ll play around to get an understanding of important functions on numbers, and also how floating point numbers (numbers with a decimal point) take over expressions when they are present.

Open the Python shell in Thonny (bottom window) and type the expressions below. Together, try to predict the output of the interpreter before pressing the ENTER key.

a = 3
x = 1.5
type( a )
type( x )
type( a * x )
type( a * 100 )
type( 1 )
type( 1.0 )
type( "1" )
a / 3
a // 3
type( a/3 )
type( 5/4 )
type( 5//4 )
type( int( 1.5 ) )
int( 1.5 )
round( 1.6 )
round( 1.4 )
round( -1.8 )
type( round( 1.4 ) )
round( -1.8 )
abs( -4 )
abs( 10 )
type( abs( -19.3 ) )
type( abs( -4 ) )

Note how once something is a float, it forces whatever it gets combined with to yield a result that is float. That is, except for the int() function, of course!

Now that you have started to understand, we will move onto the portion of the lab that you will hand in. Begin by downloading the lab starter file (click this link), and save it locally.

Update the header with the relavent information. Here is an example header:

# ------------------------------------------------------
#        Name: Ada Lovelace and Katherine Johnson
#     Section: L02
#    Filename: lab1p1.py
#       Peers: Grace Hopper
#  References: N/A
# ------------------------------------------------------


Step #1: Input Numbers

  • Write a small program (either in the Python Shell, or in the Edit window), that asks the user to enter two integers (recall the input command), and then prints out the integer division of the first number by the second number.

  • Here is a sample of what your output should look like Python Shell

  • What happens if the second number is bigger than the first number? What happens if you enter zero for one of the numbers? Create a few “test cases” to make sure that your code works in all situations.

At this point you should switch driver/navigator roles.


Step #2: Cash Machine

Begin by downloading the second starter file (click this link), and save it locally. Update the header with the relavent information.

We will write a program that takes an arbitrary amount of money (dollars and cents) and figures out how to break it down into the smallest number of 20-, 10-, 5-, and 1-dollar bills, plus change (in quarters, dimes, nickels, and pennies).

For those new to US money:

  • a quarter = 25 cents = $0.25
  • a dime = 10 cents = $0.10
  • a nickel = 5 cents = $0.05
  • a penny = 1 cent = $0.01

0: Get the original amount

  • Under the #get the initial amount comment, create a variable called amount and use it to store the value of a user input (evaluated as number). This variable should now be a float.
  • Add a print() statement under the #output number of bills comment, and make it print the amount the user wants to withdraw. This is called print()-debugging, and it is helpful in pinning down where things went wrong when we run into bugs.
  • Verify that your program works as expected.

1: dollars and cents

Life is a lot easier if we deal with dollars and cents separately: * Split the amount into dollars (an int) and cents (a float). Hint: try using the math.floor(...) function to get the dollars and subtraction to get the cents. You can also use the integer division // and modulo % functions.

2: $20 bills

When making change, we start from the largest size bill (or coin) and work our way down. In the US currency system, this minimizes the total number of bills/coins needed. In this step, you’ll compute the number of $20 bills necessary:

  • Under the # compute number of bills comment, use the correct operator (//, /, or %) to compute the number of $20 bills and store that value in a new variable, called num_20s.
  • Make your program output the num_20s variable in the output section.
  • Verify that your program works as expected.

At this point you should switch driver/navigator roles.

3: remaining amount

  • Go back to the computation of the number of $20s, and compute the amount of money left over once the $20s are taken out of the amount. There are several ways of doing this: you can do it using the % modulo operator, or using multiplication and subtraction. Whichever method you prefer is fine!
  • Store this amount in a new variable called remainder.
  • Make your program output the remainder, just to make sure that value is computed correctly.
  • Verify that your program works as expected.

4: other denominations

  • Now that you have the structure for your program, add enough Python code to make your code display:
    • The number of $20-bills
    • The number of $10-bills
    • The number of $5-bills
    • The number of $1-bills

  • Verify that your program works. Below is a typical output you should try to emulate:

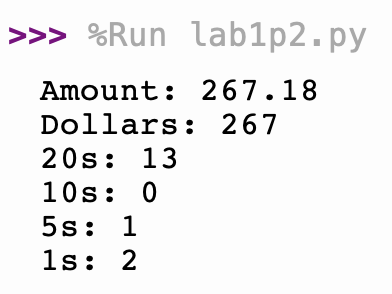
  • Try at least five different values for amount. Include a comment ## in your code, listing the values that you tested.

At this point you should switch driver/navigator roles.

5: computing coins

The coins are going to be a little trickier because operations on floats are imprecise. For example, look at what happens when you execute the following in the shell:

import math
amount = 2.19
dollars = math.floor(amount)
cents = amount - dollars
print(cents)

You’ll most likely get something that looks like this:

0.1899999999999999995

Weird, huh? This is an artifact of the limited precision of storing real numbers in finitely many bits. If you want to read more about the limitations of floating point operations in Python, check out: The Python Tutorial Chapter 15. Floating Point Arithmetic: Issues and Limitations.

For now, we’ll have to find a workaround.

  • Convert the value stored in you cents variable (which is currently a float) to an integer value using a combination of the round(...) function and multiplication by 100.
  • Using the same procedure you discovered to calculate the number of each denomination of bill, figure out how many quarters, dimes, nickels and pennies are needed to make change to this amount.
  • Update your output and check to make sure that the numbers make sense:
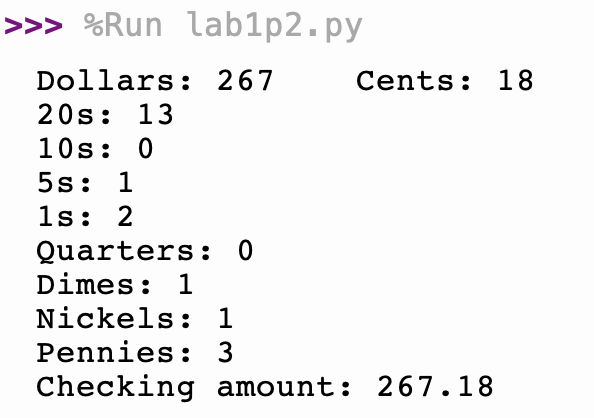
  • Go back and reuse your test values from Part 4. Does your code work for all values?

At this point you should switch driver/navigator roles.


We just learned about the limited precision of storing real numbers in finitely many bits. Take 2 minutes and discuss with your partner how this may pose a risk or issue in the real world. Have you encountered any “rounding errors” in your life?

Step #3: Grade Calculator

Begin by downloading the third starter file (click this link), and save it locally. Update the header with the relavent information.

At Smith College, the grade breakdown is as follows:

A denotes the grade 90 - 100.

B denotes the grade 80 - 89.

C denotes the grade 70 - 79.

D denotes the grade 60 - 69.

E denotes the grade 0 - 59.

1: Practise with if statements

Write a program that takes as input a number and outputs if the grade is a pass.

2: Practise with if else statements

Update your program to take as input a number and outputs if the grade is an S (Satisfactory) or a U (Unsatisfactory). For this example, we will say that 75 or above is S.

3: Practise with if elif else statements

Update your program to take as input a number and outputs the letter grade.

4: Create the Grade Calculator

Update your program to take as input either a letter grade or a number grade and converts it to the opposite. You can start from the program we wrote in class but this is insufficient.


Lab Submission